Entropie als Gesamtzufallsmenge ++ Beispiele, Bilder & Erklärung

Gesamtzufallsmenge:

( = Menge an Zufall , Zufälligkeit , statistische Entropie, )

In den meisten Statistikbüchern fehlt der Begriff Entropie völlig oder er wird nur kurz erwähnt. Das ist erstaunlich , denn die Entropie sagt etwas über die Menge an Zufall aus, die in einem oder mehreren zufälligen Ereignissen steckt und sollte somit ein Basisbegriff der Wahrscheinlichkeitsrechnung sein. Wenn er erwähnt wird , wird die Entropie dabei recht kompliziert als Erwartungswert einer Zufallsfunktion definiert .

Ich möchte im folgenden versuchen die Entropie als Menge an Zufall , bzw als Gesamtzufallsmenge an hand einfacher Beispiele klarer zu machen.

Die Gesamtzufallsmenge soll aussagen, wieviel Zufall in einem oder mehreren Ereignissen enthalten ist . Sie entspricht der Entropie in der Informationstheorie.

Achtung: Sie ist etwas anderes als die Wahrscheinlichkeit !!

Die Gesamtzufallsmenge ist 0 bei einem sicheren Ereignis oder bei einer Folge von sicheren Ereignissen.

Das erscheint plausibel, denn in einem sicheren Ereignis steckt kein Zufall
Die Wahrscheinlichkeit eines sicheren Ereignisses ist 1
Beispiel Münze mit 2 gleichen nicht unterscheidbaren Seiten .
Oder zb Folge 000000000000000

Sie ist 0 bei einem unmöglichen Ereignis

Das erscheint sehr logisch , denn in einem völlig unmöglichen Ereignis steckt kein Zufall
Wahrscheinlichkeit 0

Sie kann nicht kleiner Null sein.

Das erscheint sehr logisch , denn negativer Zufall ist kaum vorstellbar .
siehe auch negentropie

Sie ist 1 für ein Ereignis mit der Wahrscheinlichkeit 50 % / 50 % = 0,5

Diese Festlegung erscheint anfangs etwas willkürlich , ist aber doch ziemlich plausibel und akzeptierbar
Genauso gut könnte man die Zufälligkeit eines idealen Münzwurfs mit 10 oder 100 beziffern.
Beispiel ideale Münze bei einem Wurf,
Beispiel 2: Urne mit 2 verschieden farbigen , sonst identischen Kugeln bei einer Ziehung

Die Gesamtzufallsmenge hat die Einheit bit , will man Sie als Zufallsbit kennzeichen , kann man sie vielleicht als zbit bezeichnen

Da immer wieder die gesamte Informationsmenge mit der Menge an Zufall verwechselt wird , kann man vielleicht mit der Einheit zbit mehr Klarheit schaffen.

Die Gesamtzufallsmenge mehrerer unabhängiger Zufallsereignisse ist gleich der Summe der einzelnen Zufallsmengen.

Macht man mehrere Würfe mit einer idealen Münze so ist die Gesamtzufallsmenge gleich der Zahl der Würfe .
Beispiel Münze 20 mal geworfen = Gesamtzufallsmenge 20 bit
Oder in der Chaitin Reihe B steckt auch eine Gesamtzufallsmenge von 20 bit
Chaitin B: 01101100110111100010

Sie ist mit einem Wurf größer als 1

Beispielsweise bei einem 6erWürfel. Allgemein ist sie größer als eins für ein Zufallsereignis aus einem Zufallsexperiment mit mehr als 2 gleichberechtigten Möglichkeiten im Ergebnisraum . Ihr Wert wird bei gleichwahrscheinlichen Möglichkeiten im Ergebnisraum folgendermaßen berechnet : H = log₂ (Zahl der gleichberechtigten Elemente im Ergebnisraum ).

ld = lb = binärer Logarithmus = log zur Basis 2 = log₂ siehe VB Programm logarithmus

Siehe auch meine Logarithmusseite

( ein paar leichte Werte für den binären Logarithmus sind folgende: ld 1 = 0 , ld 2 = 1 , ld 4 = 2 , ld 8 = 3 , ld 16 = 4 , ld (1/2) = – 1, ld (1/4) = – 2 etc etc )

Beispiel idealer achter Würfel : 8 Möglichkeiten im Ergebnisraum daraus folgt Gesamtzufallsmenge für einmal werfen H = ld (8) = 3
Dies kann man sich dadurch verdeutlichen , wenn man den Wurf mit dem achter Würfel mit mehreren Münzwürfen nachmachen will , so braucht man genau 3 ideale Münzwürfe um 8 gleichberechtigte Möglichkeiten zu erhalten.
Da ein Münzwurf die Zufallsmenge 1 zbit hat , hat dann ein achter Würfel die Zufallsmenge 3 zbit.

Die Gesamtzufallsmenge kann eine nichtganze Zahl sein für ein Zufallsereignis aus einem Zufallsexperiment mit mehr als 2 Möglichkeiten im Ergebnisraum , bei denen die Anzahl der Elemente im Ergebnisraum nicht Vielfaches von 2 sind :

zb 6er Würfel :

6 Möglichkeiten im Ergebnisraum daraus folgt Gesamtzufallsmenge für einmal werfen H = ld 6 = ld 2*3 = ld 2 + ld3 = 1 + ld 3 = 1 + 1.58496250072116 = 2.58496250072116 zbit

Abbildung : Zusammenhang zwischen der Zahl der gleichberechtigten Möglichkeiten bei einem Zug und der Gesamtzufallsmenge = Entropie H in zbit

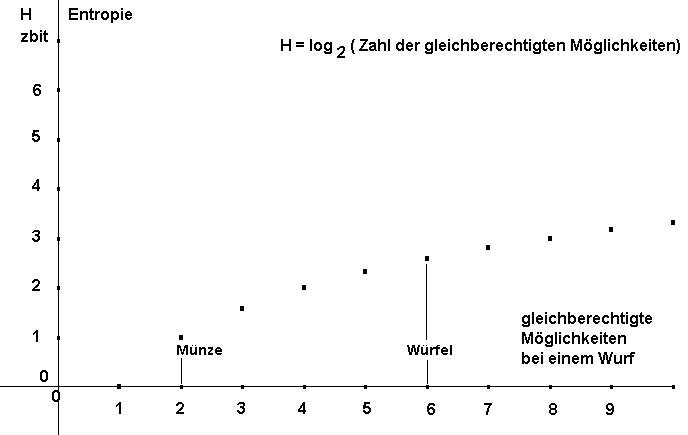
Im Urnenmodell wird es am klarsten :

Urne mit einer Kugel => Entropie = 0 , da sicheres Ereignis
Urne mit 2 verschiedenen Kugeln => Entropie = 1 / Zug = ideale Münze
Urne mit 3 verschiedenen Kugeln => Entropie = 1,5849 / Zug
Urne mit 4 verschiedenen Kugeln => Entropie = 2 / Zug = 4er Würfel (Pyramide)
Urne mit 5 verschiedenen Kugeln => Entropie = 2,3219 / Zug
Urne mit 6 verschiedenen Kugeln => Entropie = 2,58496 / Zug = 6er Würfel ( Quader)
Urne mit 7 verschiedenen Kugeln => Entropie = 2,80735 / Zug
Urne mit 8 verschiedenen Kugeln => Entropie = 3 / Zug = 8er Würfel
und so weiter bis zur Unendlichkeit

Die Gesamtzufallsmenge ist kleiner als 1 für ein Zufallsereignis aus einem Zufallsexperiment mit 2 Möglichkeiten im Ergebnisraum , wenn die Möglichkeiten im Ereignisraum nicht gleichwahrscheinlich sind.

1. Beispiel Reißnagel , der auf den Rücken oder die Spitze fällt.
- Meist fällt er öfter auf die Spitze als auf den Rücken .
- 100 Würfe durchführen. relative Häufigkeit Rückenlage berechnen
- relative Häufigkeit Spitzlage berechnen
- daraus Wahrscheinlichkeit W Rücken und W Spitze schätzen
- daraus Zufallsmenge eines Wurfes berechnen , H = – ( p * ld p + q * ld q)
- ( siehe formeln)
- daraus kann man die Gesamtzufallsmenge der 100 Würfe addieren .
- zb Wahrscheinlichkeit Rücken = 0,2
- dann ist Wahrscheinlichkeit Spitze = 0,8
- Daraus folgt die Entropie für jeden Wurf H = – ( 0,2 * ld 0,2 + 0,8 * ld 0,8)
- H = 0,2 * 2.32192809488736 + 0,8 * 0.321928094887362
- H = 0,464385618977472 + 0,2575424759098896
- H =ca 0,72 zbit
2.Beispiel : Urne mit 4 Kugeln : 1 Kugel ist schwarz ( = das schwarze Schaf ) , die anderen 3 Kugeln sind weiß
- Wahrscheinlichkeit für Weiß p = 3 / 4 , für Schwarz q = 1 / 4.
- H = – ( p * ld p + q * ld q)
- H = – ( 3/4 * ld (3/4) + 1/4 * ld ( 1/4) ) = – ( – 0,31 – 0,5 ) = 0,81 zbit
- paradox :
- Wenn man eine 2.Urne hinzunimmt mit der gegenteiligen Verteilung
- Wahrscheinlichkeit für Weiß 1 / 4 , für Schwarz 3 / 4.
- dann müßte sich das ganze zu 2 Münzwürfen ergänzen , bzw 2 Münzwürfen entsprechen.
- Leider ist das nicht ganz so wie der Abschnitt paradox zeigt
- Es funktioniert nur wenn man die Reihenfolge zwischen Urne 1 und 2 auch per Zufall festlegt.
3.Beispiel achter Würfel mit einem Feld 1 und allen anderen Feldern mit 0 gekennzeichnet :
- 2 Möglichkeiten im Ergebnisraum:
- 1 Möglichkeit hat die Wahrscheinlichkeit 1/8
- die zweite Möglichkeit hat die Wahrscheinlichkeit 7/8

Leider kann man diese Beispiele nicht so einfach mit der idealen Münze simulieren.

Auch durch wiederholten Wurf oder durch wiederholtes Ziehen aus der Urne kommen keine Vielfachen von Münzwürfen heraus .

Beim Beispiel 1 und 3 ergänzen sich die Wahrscheinlichkeiten beider Möglichkeiten zu Summe 1 , da es nur 2 Möglichkeiten gibt.

p + q = 1

Die Entropie läßt sich in diesem Fall mit folgender Formel berechnen : H = – ( p * ld p + q * ld q)

Ersetzt man in der zweiten Formel q durch den Ausdruck 1- p

So erhält man die Formel H = – ( p * ld p + ( 1- p ) * ld (1-p))

Dies kann man grafisch folgendermaßen darstellen:

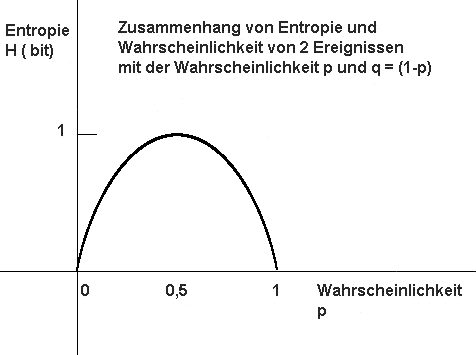
Für jedes p kann man daraus die Entropie direkt ablesen. Die Funktion ist symmetrisch zur Geraden p = 0,5 . Sie fällt bei p = 0 sehr steil zu einem Entropie Wert von = 0 ab . Auch bei p Werten, die sich dem sicheren Ereignis von p = 1 nähern fällt die Entropie auf 0 ab.

Dieser Zusammenhang gilt jeweils für ein Zufallsereignis . Bei mehreren Zufallsereignissen muß man natürlich wieder die einzelnen Entropien zusammenzählen und man kann so leicht Entropiewerte über 1 erreichen.

Die Wahrscheinlichkeit p dagegen bleibt auch bei Wiederholungen definitionsgemäß immer zwischen 0 und 1 !

Urne ohne Zurücklegen

Wie berechnet sich die Entropie bei einer Urne mit 8 verschiedenen Kugeln , wenn man die Kugeln nicht zurücklegt und hintereinander alle Kugeln zieht ?

Gesamt H = ld 8 + ld 7 + ld 6 + ld 5 + ld 4 + ld 3 + ld 2 + ld 1 = ld (1*2*3*4*5*6*7*8) = ld (8!) = ca 15.2 zbit .

Die errechnete Gesamtzufallsmenge steckt in der Zufälligkeit der Reihenfolge der verschieden farbigen 8 Kugeln.

Stimmt diese Rechnung ? ja

Entropie bei mehr als 2 Möglichkeiten mit ungleichen Wahrscheinlichkeiten im Ergebnisraum.

zb Urne mit 8 Kugeln : 4 schwarze , 2 weiße , 1 rote , 1 blaue = 4s,2w,1r,1b

Wahrscheinlichkeiten : ps = 1/2 , pw = 1/4 , pr = 1/8 , pb = 1/8

Wie groß ist die Entropie pro Zug ?

Die dafür gültige Formel lautet : H = – ( p1* ld (p1) + p2 * ld (p2) + p3 * ld (p3 ) + …… pn * ld (pn) ) = – Summe ( 1 bis n ) von pn * ld(pn) = – å p_n* ld(p_n)

Das Beispiel berechnet sich also folgendermaßen:

H = – ( 1/2 * ld(1/2) + 1/4 * ld(1/4) + 1/8 * ld ( 1/8) + 1/8 * ld ( 1/8) )

H = – ( 1/2 * ( – 1) + 1/4 * (-2) + 1/8 * (-3) + 1/8 * (-3) )

H = 1/2 + 2/4 + 3/8 + 3/8

H = 4/8 + 4/8 + 3/8 + 3/8

H = 14/ 8 = 7/4

Schwieriger wird es wenn sich die Wahrscheinlichkeiten nicht zur Summe 1 addieren !

Paradox: Schwierigkeiten mit der Vorstellung der Gesamtzufallsmenge

Man muß bei der Berechnung oder Abschätzung der Gesamtzufallsmenge für kombinierte oder gemischte Zufallsereignisse sehr aufpassen , daß man nicht irgendwelchen Fehlschlüßen aufsitzt.

Beispiel: 2 Urnen mit Wahrscheinlichkeit 1/4 und 3/4 und gleichen Kugelfarben.

( S = Schwarze Kugel , W = Weiße Kugel )

Urne 1: S,W,W,W

Urne 2: W,S,S,S

Dann möchte man annehmen, daß sich die beiden Effekte zur Wahrscheinlichkeit 0,5 ausgleichen, wenn man aus beiden Urnen zieht. In der Summe müßte beides also 2 Münzwürfen entsprechen. Man sollte als Ergebnis die Entropie 2 bekommen, wenn man aus beiden Urnen zieht.

==> Leider ist das nicht so , wie folgende Programmierung zeigt:

Wenn man beide Urnen zusammenschüttet würde es klappen . Mit 2 getrennten Urnen klappt es nicht . Warum ist das so ? Eine Programmierung klärt das Problem auf:

Man programmiert 2 unabhängige 4er Urnen mit den Möglichkeiten 1,2,3,4.

Bei Urne 1 legt man für 1 als Ergebnis die Zahl 0 fest , allen anderen 3 Möglichkeiten erhalten die Zahl 1 zugeordnet .

Bei Urne 2 kehren sich die Verhältnisse um . Für die 1 als Zufallszahl ordnet man 1 als Ergebnis zu , die 2,3 und 4 bekommen die 0 zugeordnet .

Folgender Programmcode in Visual Basic erläutert das Ganze nochmal.

Sub Befehl20_Click ()

Randomize Timer
Dim t As String
Dim ui As Integer
Dim uk As Integer
For x = 1 To 3000 : Rem beliebige Zahl als obere Grenze
- ui = Int(4 * Rnd + 1) ‚ Erzeugt einen Wurf zwischen 0 und 3
- If ui = 1 Then t = t & „0“
- If ui = 2 Then t = t & „1“
- If ui = 3 Then t = t & „1“
- If ui = 4 Then t = t & „1“
- uk = Int(4 * Rnd + 1)
- If uk = 1 Then t = t & „1“
- If uk = 2 Then t = t & „0“
- If uk = 3 Then t = t & „0“
- If uk = 4 Then t = t & „0“
Next x
text1.Text = t

End Sub

Läßt man nun diese 2 Zufallsprozeße mehrfach in einer Schleife ablaufen und testet das Ergebnis statistisch mit dem Programm stat01 prg01st.htm , dann erkennt man zwar eine statistisch ungefähr gleiche Zahl von 0 und 1 . Bei den Paaren 11,01,10,00 fällt aber ein völliges Ungleichgewicht auf.

Durch die immer geordnete Reihenfolge von Zufallsprozeß 1 , danach Zufallsprozeß 2 wird die Gesamtzufälligkeit gegenüber 2 Münzwürfen reduziert. Erst wenn man auslost , wer zuerst kommt Zufallsprozeß 1 oder 2 , spielt die Reihenfolge keine Rolle mehr und es stellt sich eine saubere Zufallsfolge für 0 und 1 ein.

Der dazu gehörige Code schaut dann anders aus :

Sub Befehl21_Click ()

Randomize Timer
Dim t As String
Dim ui As Integer
Dim uk As Integer
For x = 1 To 2000
- m% = Int(2 * Rnd) ‚ Erzeugt einen Wurf zwischen 0 und 1
  - If m% = 0 Then GoSub uisub
  - If m% = 1 Then GoSub uksub
Next x
GoTo weiter ‚ Hinter die Unterprogramme springen.
uisub:
- ui = Int(4 * Rnd + 1) ‚ Erzeugt einen Wurf zwischen 0 und 3
  - If ui = 1 Then t = t & „0“
  - If ui = 2 Then t = t & „1“
  - If ui = 3 Then t = t & „1“
  - If ui = 4 Then t = t & „1“
Return
uksub:
- uk = Int(4 * Rnd + 1)
  - If uk = 1 Then t = t & „1“
  - If uk = 2 Then t = t & „0“
  - If uk = 3 Then t = t & „0“
  - If uk = 4 Then t = t & „0“
Return
weiter:
- text1.Text = t

End Sub

Erst die Kombination

2er Urne

4er Urne (1w 3s) oder 4er Urne (3w 1s)

ergibt in der Summe die Entropie 2 . Das entspricht 2 mal einer 2er Urne oder 2 Münzwürfen.

paradox 2: Wenn man über folgende Formel H = – p * log₂(p) die Entropie aus einer gegebenen Wahrscheinlichkeit berechnet, ergibt sich Erstaunliches :

Wahrscheinlichkeit : p = 1/2 ==> H = 1/2 = 0,5
Wahrscheinlichkeit : p = 1/3 ==> H = ca 0,528 also größer als 0,5 !!!
Wahrscheinlichkeit : p = 1/4 ==> H = 1/2
Wahrscheinlichkeit : p = 1/8 ==> H = 3/8

Für die Wahrscheinlichkeit 1/2 und 1/4 ergeben sich identische Entropiewerte von 0,5 bit , für dei Wahrscheinlichkeit 1/3 ergibt sich so gar ein Entropiewert der größer als 0,5 ist.

Abbildung : Funktion Entropie vs. Wahrscheinlichkeit : H = – p * ld (p) = – p * log₂(p)

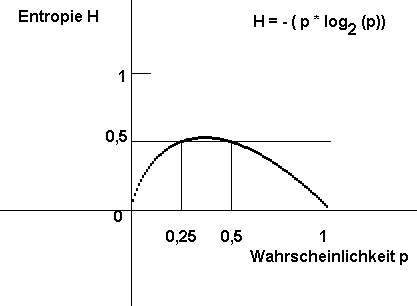
Beachte : Diese Funktion ist nicht symmetrisch zu x = 0,5 , und sie hat ein Maximum für einen x Wert kleiner als 0,5 und einen y Wert größer als 0,5 !!

Wie ist dieses auf den ersten Blick paradoxe Ergebnis zu erklären ?

Man kann es sich mit folgender Überlegung klar machen :

2er Urne:

Habe ich eine Urne mit 2 gleichberechtigten Möglichkeiten , dann ist p = 1/2 .
Die Gesamtentropie ist 1 , die Teilentropie für jede Möglichkeit = 1/2 * 1 = 0,5

3er Urne:

Habe ich eine Urne mit 3 gleichberechtigten Möglichkeiten , dann ist p = 1/3 .
Die Gesamtentropie pro Zug ist H = ld 3 = 1,5849
Die Teilentropie für jede einzelne Möglichkeit h = Gesamtentropie H / 3 = 1/3 * ld 3 = ca 0,528

4er Urne:

Habe ich eine Urne mit 4 gleichberechtigten Möglichkeiten , dann ist p = 1/4 .
Die Gesamtentropie pro Zug ist H = ld 4 = 2
Die Teilentropie für jede einzelne Möglichkeit h = Gesamtentropie H / 4 = 1/4 * ld 4 = 0,5

Obige Grafik ist also nur richtig für die Teilentropie bezogen auf die einzelne Möglichkeit , nicht auf die Gesamtentropie pro Zug.

Zusammenhang Gesamtzufallsmenge und Wahrscheinlichkeit

Der Zusammenhang zwischen der Wahrscheinlichkeit und der Entropie ist nicht immer sofort offensichtlich.

Wenn man ein Zufallsexperiment mit bekannter Wahrscheinlichkeit mehrfach wiederholt , dann bleibt die Wahrscheinlichkeit immer gleich , die Gesamtentropie der Folge wächst an und kann aus der Wahrscheinlichkeit und der Zahl der durchgeführten Experimente berechnet werden.

Wenn man ein Zufallsexperiment mit unbekannter Wahrscheinlichkeit mehrfach wiederholt , dann wird die Wahrscheinlichkeit immer besser und genauer bestimmbar. Die Gesamtentropie der Folge wächst an und kann aus der geschätzten Wahrscheinlichkeit und der Zahl der durchgeführten Experimente berechnet werden.

Wann nimmt man welche Formel ?

Entropieformeln für den Zusammenhang Entropie H als Funktion der Wahrscheinlichkeit p

H = f ( p)

allgemeine Formel

Formel für die Teilentropie p

H = – p * log₂(p)
siehe paradox 2

Formel für 2 komplementärer Ereignisse mit den Teilwahrscheinlichkeiten p und q und der Gesamtwahrscheinlichkeit 1. p + q = 1

H = – ( p * ld p + q * ld q)

Summe der Entropie von unabhängigen Ereignissen

Internetseiten zum Thema Zufall

http://www.eduvinet.de/gebhardt/stochastik/zufallsg.html ***

http://home.wtal.de/schwebin/lsys/zufall.htm**

http://www.random.org liefert echte Zufallszahlen

http://webnz.com/robert/true_rng.html

Seiten über echte Hardware Zufallszahlengeneratoren

http://www-math.uni-paderborn.de/~aggathen/vorl/2001ss/sem/

http://www.uni-koblenz.de/~hasan/zufall/zufall.html

Universität Koblenz-Landau, Abt. Koblenz Fachbereich Informatik
Proseminar im WS 97/98 von Sasa Hasan
Zufallszahlen
Inhalt
Einleitung
Methoden zur Erzeugung von Zufallszahlen
Linear kongruente Methode
Andere Methoden
Testen von Folgen von Zufallszahlen
-Test
Kolmogorov-Smirnov-Test
Anmerkungen zum Spektral-Test
Nicht-gleichverteilte Zufallszahlen
Literaturangaben

http://www.uni-ulm.de/~cschmid/v2000s/webprob/sb1/sb1_2.htm

Schöne Seite über Zufallsgeneratoren mit vielen Bildern
§1 Einführung: Was ist Zufall?
§2 Pseudozufallszahlen
§3 Einige mathematische Grundlagen
§4 Lineare Kongruenzgeneratoren
§5 Simulation der Gleichverteilung
§6 Simulation der Dreiecksverteilung
§7 Simulation der Gauß-Verteilung

http://random.mat.sbg.ac.at/

http://www.fh-weingarten.de/iaf/projekte/is/zufall.htm

http://www.romankoch.ch/capslock/zufall.htm

http://www.paroli.de/roulette/index.htm

http://www.uni-klu.ac.at/stochastik.schule/

http://www.dartmouth.edu/~chance/index.html

Sehr schöner Kurs zum Thema Zufall in Englisch

http://www.philosophiebuch.de/lassonzu.htm

http://cdl.library.cornell.edu/Hunter/hunter.pl?handle=cornell.library.math/00660001&id=5

Die Analyse des Zufalls by Timerding, Heinrich Emil
1.Kap: Der Begriff des Zufalls S1
2.Kap: Die statistische Methode S13
3.Kap: Stationäre Zahlenreihen S21
4.Kap: Das Gesetz der großen Zahl S35
5.Kap: Die Theorie der Glücksspiele S50
6.Kap: Die Mathematische Analyse stationärer Reihen S69
7.Kap: Das Urnenschema S91
8.Kap: Näherungsformeln S105
9.Kap: Die statistische Theorie des Zufalls S134
10.Kap: Die genetische Theorie des Zufalls S154
Namensverzeichnis

Internetseiten zum Thema Stochastik

http://www.mathematik.uni-kassel.de/didaktik/biehler/StatistikOnline/index.html

Gute Übersicht zu weiteren Links

AK Stochastik in der Schule der GDM

Hompage Prof. Dr. Biehler, Uni Kassel

Mathematik und Informatik, PH Ludwigsburg

Statistik an der Universität Klagenfurt

Educational Statistik an der Universität Wien

Statistik-Seiten an der Universität Köln

http://www.zufallsgeneratoren.de/

http://www.fortuna-service.de/home.html

http://www.math.psu.edu/gunesch/entropy.html

http://stargate.cosy.sbg.ac.at/pherbert/monte/monte.htm**

http://www.uni-magdeburg.de/zoellner/ma_zufall.html

http://www.darmstadt.gmd.de/BV/BI-Esto1.html

http://math-www.uni-paderborn.de/~aggathen/vorl/2001ss/sem/

http://www.cmap.polytechnique.fr/~bousquet/kolmogorov.html

Sicherlich kennen Sie auch folgenden Aufsatz von Pincus und Kalman aus dem Jahr 1997, der ein Meilenstein in der Forschung gewesen ist: http://www.pnas.org/cgi/content/full/94/8/3513**

Leider ist das Programmlisting nicht dabei.

http://late5.e-technik.uni-erlangen.de/user/fo/esp.htm

http://dcbwww.unibe.ch/groups/schumacher/happy.html

Schönes Gasmodell

http://www.mathematik.uni-muenchen.de/~duerr/Zufall/zufall.html